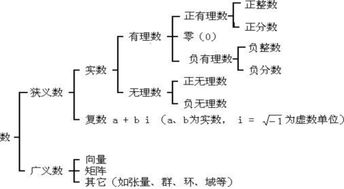
实数包括哪些数?
实数的定义
实数包括所有有理数和无理数。有理数是可以表示成两个整数之比的数,包括整数、分数、小数等。无理数是不能表示成两个整数之比的数,例如π和sqrt(2)等。有理数和无理数的例子
有理数: - 整数:1、2、3、4、5、6... - 分数:1/2、3/4、5/6... - 小数:0.1、0.5、1.0... 无理数: - π:圆周率,约为3.14159265358979323846... - sqrt(2):根号2,约为1.41421356237309507... - e:自然对数的底,约为2.718281828459047...有理数和无理数的运算
有理数和无理数可以进行加、减、乘、除等运算,其结果分别为: - 有理数加减法:1+2=3,2+3=5,3+4=7... - 有理数乘除法:2*3=6,3*4=12,4*5=20... - 无理数加减法:pi+sqrt(2)=sqrt(pi^2+2),pi-sqrt(2)=sqrt(pi^2-2)..." - 无理数乘除法:sqrt(2)*pi=sqrt(2)pi,pi*sqrt(2)=pi^2/2..."实数的应用
实数在日常生活和各个领域都有广泛的应用,例如: - 数学:实数是数学的基础,包括代数、几何、微积分等。 - 物理:实数在物理中用于描述物理量,如温度、速度、加速度等。 - 计算机科学:实数可以用于计算机中的数据类型,如整数、浮点数等。 - 经济学:实数可以用于经济学中的数据分析,如收入、物价、利率等。实数的奇偶性
实数具有奇偶性,即: - 有理数奇偶性:有理数可以分为奇数和偶数两类,分别为正有理数和负有理数。 - 无理数奇偶性:无理数没有明显的奇偶性。实数的运算性质
实数具有以下运算性质: - 加法结合律:对于任意实数a、b、c,(a+b)+c=a+(b+c)。 - 加法交换律:对于任意实数a、b,a+b=b+a。 - 加法单位元:对于任意实数a,1+a=a+1=0+a=a。 - 乘法结合律:对于任意实数a、b、c,(a*b)*c=a*(b*c),(b*c)*a=b*(c*a),(a*b)*c=a*(b*c)。 - 乘法交换律:对于任意实数a、b,a*b=b*a。 - 乘法单位元:对于任意实数a,1*a=a*1=0*a=a。声明：内容来自互联网不代表本站观点，转载请注明：https://bk.66688831.com/13/168671.html